R:Статистическая проверка принадлежности нормальному распределения — различия между версиями
м (→Маленькие хитрости) |
м (→Применение функций к нескольким по группам) |
||
| Строка 223: | Строка 223: | ||
<syntaxhighlight lang="rsplus"> | <syntaxhighlight lang="rsplus"> | ||
| − | > DF$GRP <- sample(LETTERS[1:3], size = 100, replace = TRUE) | + | > DF$GRP <- factor(sample(LETTERS[1:3], size = 100, replace = TRUE)) |
</syntaxhighlight> | </syntaxhighlight> | ||
Версия 14:52, 15 февраля 2014
| |
Материал «R:Статистическая проверка принадлежности нормальному распределения», созданный автором Артём Клевцов, публикуется на условиях лицензии Creative Commons «Attribution» («Атрибуция») 4.0 Всемирная. | |
|
Предположение о принадлежности случайной величины нормальному закону распределения лежит в основе многих статистических методов и критериев. В ряде случаев соблюдение данного требования является критичным для применения того или иного метода.
На практике мы встречаемся с двумя вариантами задач по проверке принадлежности распределения нормальному закону: для одномерного и многомерного распределения.
| Перед использованием функций из пакетов их необходимо предварительно установить и загрузить: <syntaxhighlight lang="rsplus">
> install.packages(pkgs = "pkgname") > library(package = "pkgname") </syntaxhighlight> |
Содержание
Одномерное нормальное распределение
В качестве [math]H_0[/math] для всех нижеприведённых критериев является предположение, что «случайная величина [math]X[/math] распределена нормально».
Для демонстрации работы функций, реализующий различные критерий проверки принадлежности распределения нормальному закону сгенерируем вектор случайных чисел, имеющих стандартное нормальное распределение:
<syntaxhighlight lang="rsplus"> > x <- rnorm(n = 100) </syntaxhighlight>
Статистические критерии
Пакет stats
В данном пакете реализованы две функции, которые позволяют осуществить проверку принадлежности распределения нормальному закону.
-
shapiro.test- критерий Шапиро - Уилка -
ks.test- критерий Колмогорова - Смирнова[1]
Данные функции возвращают результат в виде S3-класса - htest.
Пакет nortest
В данный пакет входят следующие функции:
-
ad.test- критерий Андерсона - Дарлинга -
cvm.test- критерий Крамера - фон Мизеса -
lillie.test- критерий Лиллиефорса -
pearson.test- критерий [math]\chi^2[/math] Пирсона -
sf.test- критерий Шапиро - Франчия
Данные функции возвращают результат в виде S3-класса - htest.
Пакет moments
В данный пакет входят следующие функции:
-
agostino.test- критерий Д'Агостино -
bonett.test- критерий Бонетта – Сайера -
jarque.test- критерий Жарка-Бера
Данные функции также возвращают результат в виде S3-класса - htest.
Пакет fBasics
В данном пакете не предлагается никакой оригинальной реализации критериев - код в основном заимствован из пакетов stats, nortest, moments. Данный пакет предлагает альтернативный вывод результатов в виде объекта S4-класса fHTEST, в том время как все предыдущие функции использовали S3-класс htest.
Функция normalTest() является «обёрктой» для ряда функций из того же пакета - fBasics. Задать необходимый критерий можно задать с помощью аргумента method. Доступны следующие критерии:
-
sw- критерий Шапиро - Уилка -
jb- критерий Жарка-Бера -
ks- критерий Колмогорова - Смирнова -
da- критерий Д'Агостино -
ad- критерий Андерсона - Дарлинга.
Пример вызова данной функции:
<syntaxhighlight lang="rsplus"> > normalTest(x, method = "sw")
Title:
Shapiro - Wilk Normality Test
Test Results:
STATISTIC: W: 0.9831 P VALUE: 0.2301
Description:
Fri Feb 14 19:59:59 2014 by user:
</syntaxhighlight>
Помимо функции normalTest() данный пакет включает в себя следующие функции:
-
shapiroTest- критерий Шапиро - Уилка -
ksnormTest- критерий Колмогорова - Смирнова[2] -
jarqueberaTest- критерий Жарка-Бера -
dagoTest- критерий Д'Агостино -
adTest- критерий Андерсона - Дарлинга -
cvmTest- критерий Крамера - фон Мизеса -
lillieTest- критерий Лиллиефорса -
pchiTest- критерий Пирсона -
sfTest- критерий Шапиро - Франчия
Данные функции также возвращают результат в виде S4-класса - fHTEST.
Пакет TeachingDemos
Данные пакет содержит только одну функцию, имеющую отношение к критериям проверки принадлежности распределения нормальному закону - SnowsPenultimateNormalityTest(). Данная функция возвращают результат в виде S3-класса - htest.
Пакет tseries
Данный пакет содержит только одну функцию, имеющую отношение к критериям проверки принадлежности распределения нормальному закону - jarque.bera.test, которая является реализацией критерия Жарка-Бера. Данная функция возвращают результат в виде S3-класса - htest.
Пакет lawstat
В данный пакет входят следующие функции:
-
rjb.test- критерий Жарка-Бера -
sj.test- SJ-критерий
Маленькие хитрости
Применение функций к нескольким переменным
С помощью apply-функций можно последовательно применить функцию к вектору, списку или массиву. Прежде чем всего нам необходимо сформировать таблицу данных. С помощью функции replicate() сгенерируем 10 переменных, имеющих стандартное нормальное распределение, которые объединяются в класс data.frame.
<syntaxhighlight lang="rsplus"> > DF <- data.frame(replicate(n = 10, rnorm(n = 100))) </syntaxhighlight>
Структура сгенерированной таблицы выглядит следующим образом:
<syntaxhighlight lang="rsplus"> > str(DF) 'data.frame': 100 obs. of 10 variables:
$ X1 : num 1.051 1.08 -0.477 -1.396 3.423 ... $ X2 : num -0.602 2.29 -0.758 -1.615 -0.364 ... $ X3 : num 0.0559 -1.0117 0.5242 0.4105 -0.3191 ... $ X4 : num -0.0965 0.2006 0.29 0.7702 -0.0182 ... $ X5 : num -0.7074 -1.6111 0.3478 0.2504 0.0609 ... $ X6 : num -1.432 0.535 -0.932 0.581 -1.606 ... $ X7 : num -1.42407 -0.31827 -2.04648 -0.19856 0.00301 ... $ X8 : num 0.511 0.192 0.467 -1.308 2.496 ... $ X9 : num -0.8508 0.4481 -0.2828 -0.5464 0.0605 ... $ X10: num 1.421 0.408 1.254 -0.956 -1.91 ...
</syntaxhighlight>
Для решения поставленной задачи можно воспользоваться функцией sapply(). Но прежде, нам необходимо немного отформатировать формат вывода результатов нашей функции: нам нужно извлечь значения критерия и его уровень значимости, т.к. результат функции shapiro.test() содержит также информацию, которая не подлежит включению в таблицу.
<syntaxhighlight lang="rsplus"> > shapiro.test(x)
Shapiro-Wilk normality test
data: x W = 0.9903, p-value = 0.6882 </syntaxhighlight>
Структура результата применения функции shapiro.test() представлена ниже:
<syntaxhighlight lang="rsplus"> > str(shapiro.test(x)) List of 4
$ statistic: Named num 0.99 ..- attr(*, "names")= chr "W" $ p.value : num 0.688 $ method : chr "Shapiro-Wilk normality test" $ data.name: chr "x" - attr(*, "class")= chr "htest"
</syntaxhighlight>
Как видим, помимо значений критерия и уровня значимости здесь содержится информация о применяемом методе. Мы можем отфильтровать вывод следующим образом:
<syntaxhighlight lang="rsplus"> > normTest <- function (x) { + res <- shapiro.test(x) + return(c(res$statistic, p.value = res$p.value)) + } </syntaxhighlight>
Результат теперь будет выглядеть следующим образом:
<syntaxhighlight lang="rsplus"> > normTest(x)
W p.value 0.9903 0.6882
</syntaxhighlight>
Теперь можно использовать данную функцию при обработке столбцов нашей таблицы.
<syntaxhighlight lang="rsplus"> > t(sapply(DF, normTest))
W p.value
X1 0.9831 0.2301 X2 0.9936 0.9213 X3 0.9800 0.1333 X4 0.9829 0.2219 X5 0.9874 0.4625 X6 0.9862 0.3874 X7 0.9839 0.2617 X8 0.9833 0.2360 X9 0.9915 0.7834 X10 0.9808 0.1531 </syntaxhighlight>
Того же результата можно добиться и с помощью функции lapply()[3]:
<syntaxhighlight lang="rsplus"> > do.call(rbind, lapply(DF, normTest))
W p.value
X1 0.9831 0.2301 X2 0.9936 0.9213 X3 0.9800 0.1333 X4 0.9829 0.2219 X5 0.9874 0.4625 X6 0.9862 0.3874 X7 0.9839 0.2617 X8 0.9833 0.2360 X9 0.9915 0.7834 X10 0.9808 0.1531 </syntaxhighlight>
Применение функций к нескольким по группам
Добавим к нашей таблицы группы испытуемых:
<syntaxhighlight lang="rsplus"> > DF$GRP <- factor(sample(LETTERS[1:3], size = 100, replace = TRUE)) </syntaxhighlight>
Рассчитаем значения критерия Шапиро - Уилка для первого столбца для каждоый группы испытуемых:
<syntaxhighlight lang="rsplus"> > do.call(rbind, tapply(DF$X1, DF$GRP, normTest))
W p.value
A 0.9522 0.13281 B 0.9607 0.28697 C 0.9410 0.07256 </syntaxhighlight>
Графические методы
Многие исследователи также используют графические методы для определения степени отклонения распределения от нормального закона. В R реализована возможность построения Q-Q и P-P графиков, гистограмм и кривых распределения плотности вероятностей.
Пакет stats
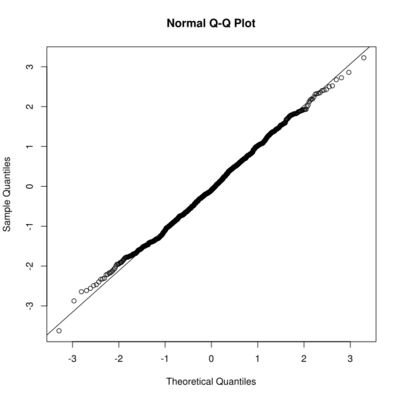
Построение Q–Q plot с помощью пакета stats выглядит следующим образом:
<syntaxhighlight lang="rsplus"> > qqnorm(x) > qqline(x) </syntaxhighlight>
Пакет QTLRel
Построение Q–Q plot с помощью пакета QTLRel выглядит следующим образом:
<syntaxhighlight lang="rsplus"> > qqPlot(x, x = "norm") </syntaxhighlight>
Пакет car
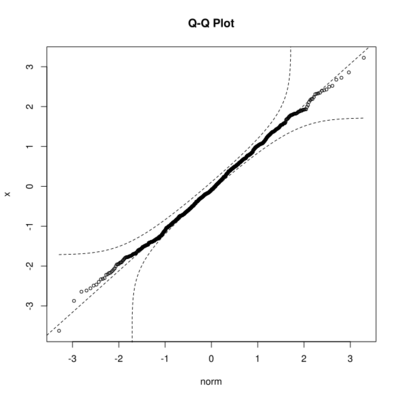
Альтернативный вариант реализован в функции qqPlot() из пакета car:
<syntaxhighlight lang="rsplus"> > qqPlot(x, distribution = "norm") </syntaxhighlight>
Пакет e1071
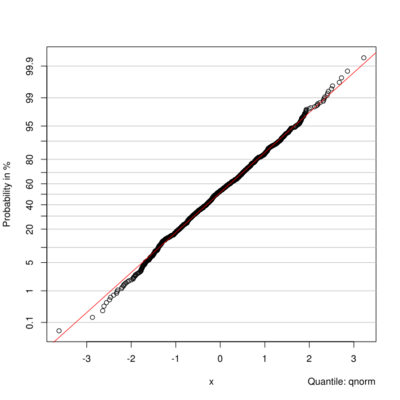
Построение P-P plot можно осуществить с помощью функции probplot из пакета e1071:
<syntaxhighlight lang="rsplus"> > probplot(x, qdist = qnorm) </syntaxhighlight>
Пакет gamlss
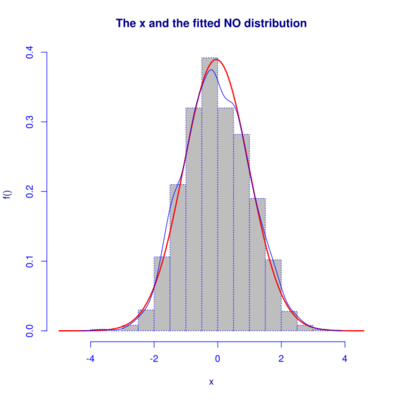
Ещё один интересный способ графического анализа представлен функцией histDist из пакета gamlss:
<syntaxhighlight lang="rsplus"> > histDist(x, family = "NO", density = TRUE)
Family: c("NO", "Normal") Fitting method: "nlminb"
Call: gamlssML(y = y, family = "NO", formula = x)
Mu Coefficients: [1] -0.2273 Sigma Coefficients: [1] 0.09813
Degrees of Freedom for the fit: 2 Residual Deg. of Freedom 98
Global Deviance: 303.414
AIC: 307.414
SBC: 312.624
</syntaxhighlight>
С помощью аргумента family можно задать семейство распределений для подгонки и сравнения[4].
Многомерное нормальное распределение
Примечания
- ↑ Для оценки нормальности вызов выглядит следующим образом:
ks.test(x, y = "pnorm") - ↑ Данная функция вызывает
ks.test(x, "pnorm")для трёх альтернативных гипотез - двусторонней и двух односторонних. - ↑ По результатам сравнения производительности, данный вариант оказался чуть быстрее предыдущего.
- ↑ Более подробную информацию о доступных семействах распределений можно получить с помощью команды
help("gamlss.family").